Table of Contents
BIVARIATE CROSS-CLASSIFIED MODEL
The previous example illustrated a research design in which a single outcome variable was measured from students who were simultaneously nested within primary and secondary schools, leading to a cross-classified dependency structure. The current example is also a cross-classified model, but with two observed outcome variables at the lowest level. This design allows us to examine the relationship between these variables at each level of the model.
Motivating Example
Our example draws on a common research paradigm in social and cognitive psychology known as the stimulus-sampling designs. In these studies, participants (raters) respond to a series of randomly sampled stimuli (targets). Specifically, responses are simultaneously nested within raters and targets, leading to a cross-classified dependency structure. Treating these sources of non-independence as random effects allows the results to generalize to the larger populations from which these stimuli were drawn (Judd, Westfall, & Kenny, 2012). In the present example, we use data collected from a sample of 243 undergraduate students who evaluated the symmetry (SYM) and physical attractiveness (PA) of male and female faces in photographs (Langner et al., 2010). Our initial model features a decomposition of SYM and PA ratings into rater- and target-specific variance components and latent correlations between PA and SYM for each of these sources. Response-specific residuals will also be allowed to correlate.
Unlike the standard analytic approach which confounds these distinct sources of variability in photo ratings, the current approach answers precise research questions that are specific to each class of variance component. Specifically, the correlation between rater variance components describes the extent to which individuals who evaluate all photographs as consistently more or less symmetrical, tend to also rate all photographs as more or less attractive. Moreover, the correlation between target variance components expresses the degree to which target photographs that are evaluated by all raters as consistently more or less symmetrical, are also rated as more or less attractive. Finally, the correlation between response-specific residuals reflects idiosyncratic associations between symmetry and attractiveness.
Bivariate Cross-Classified Random Intercepts Model
In this case, each rating is simultaneously nested within raters (participants) and targets (photographs). As a result, the symmetry and attractiveness rating is subject to three distinct sources of influence: (1) rater-effects, (2) target-effects, and (3) idiosyncratic effects, which are confounded with measurement error. The following model makes the idea of two sources of systematic influence explicit.
MLM notation
For a response \( (i) \), provided by rater \( (u) \) and evaluating target \( (v) \), the level-1 equations are:
\[ SYM_{i(u,v)} = \nu_{SYM} + 1 \times \eta^R_{SYM,u} + 1 \times \eta^T_{SYM,v} + e_{SYM,i(u,v)}, \]
\[ PA_{i(u,v)} = \nu_{PA} + 1 \times \eta^R_{PA,u} + 1 \times \eta^T_{PA,v} + e_{PA,i(u,v)}, \]
\[ e \sim N(0,\theta) \]
\[ \eta^R \sim N(0,\psi^R) \]
\[ \eta^T \sim N(0,\psi^T) \]
\( (\eta^R) \) and \( (\eta^T) \) are the unobserved latent variables representing the effects of rater and target, respectively, on symmetry and attractiveness responses.. The actual effect for a given response i depends on the specific combination of the rater and the target (\( (u) \) & \( (v) \)) involved in the evaluation. It is assumed that the effects sources of influence are independent (uncorrelated).
The model has eleven parameters:
- Grand-mean or the intercept for symmetry \( (\nu_{SYM}) \) and attractiveness \( (\eta_{PA}) \).
- Response level residual variances (\( (\theta_{SYM}) \) & \( (\theta_{PA}) \)) and covariance \( (\theta_{SYM,PA}) \)
- Rater level latent factor variances (\( (\psi^R_{SYM}) \) & \( (\psi_{PA}^R) \)) and covariance \( (\psi_{SYM,PA}^R) \) for symmetry and attractiveness.
- Target level latent factor variances (\( (\psi_{SYM}^T) \) & \( (\psi_{PA}^T) \)), and covariance \( (\psi_{SYM,PA}^T) \) for symmetry and attractiveness.
General notation
The above equations using superscripts R and T clarify the effects of raters and targets on multivariate responses. However, it is useful to think of these models in more general terms. The general notation is useful in understanding more complex models with observed and latent variables at multiple levels. For this reason, we will use numeric superscripts.
The model has three levels:
1. response
2. rater
3. target
The above equation can be re-written using numeric superscripts to specify the level information as:
\[ y^1_{pi(u,v)} = \nu^1_p + 1_{piu} \times \eta^2_{p(u)} + 1_{piv} \times \eta^3_{p(v)} + e^1_{p,i(u,v)}, \]
Here, we use superscript 1 for the dependent variable Y_p measured at the lowest level (response) and superscripts 2 and 3 for the corresponding random-intercepts for rater (2) and target (3) levels, respectively. For two dependent variables, we can re-write the above equation as:
\[ y^1_{1i(u,v)} = \nu_1^1 + 1_{1iu} \times \eta^2_{1,u} + 1_{1iv} \times \eta^3_{1,v} + e^1_{1i,(u,v)}, \]
\[ y^1_{2i(u,v)} = \nu_2^1 + 1_{2iu} \times \eta^2_{2,u} + 1_{2iv} \times \eta^3_{2,v} + e^1_{2i(u,v)}, \]
Or, more generally we could use a multivariate version that eliminates the subscript for variable:
\[ y^1_i = \nu^1 +\Lambda^{1,2} \times \eta^2_j + \Lambda^{1,3} \times \eta^3_k + e^1_i, \]
We can now express distributional assumptions regarding random-effects and residuals as:
\[ e^1 \sim N(0,\Theta^{1,1}) \]
\[ \eta^2 \sim N(0,\Psi^{2,2}) \]
\[ \eta^3 \sim N(0,\Psi^{3,3}) \]
Path Diagram
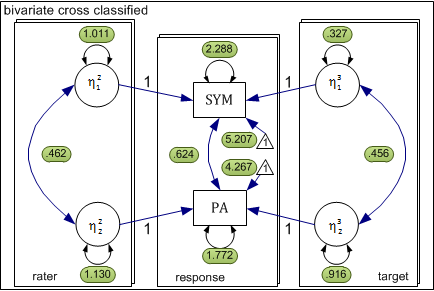
The above model can be conceptualized as a three level xxM model shown in the following diagram. In this case, the three levels are response, rater, and target. The response level is nested simultaneously within rater and target levels. For each level, there is a separate submodel delineated by a rectangle.
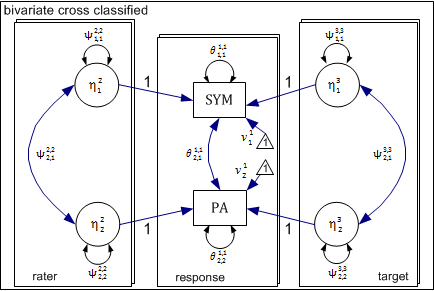
At the response level, we have two observed dependent variables and no latent variables. The remaining two levels each have two latent variables representing rater and target effects for symmetry and attractiveness. Each of these latent variables influences the response level outcome as indicated by the directional arrow. Consistent with the above equations, the coefficient (factor-loading) linking each latent variable to the observed response is fixed to 1.0.
XXM Model Matrices
The above model can be described more conveniently in matrix notation. As described earlier, we will use super-scripts to indicate level and subscripts to indicate variables. Within-level matrices for each of the three levels (response, rater, and target) are presented first, followed by across-level matrices connecting the rater (level-2) and target (level-3) levels with the response level (level-1).
Level-1 (Response): Within matrices
Level-1 is the response level. There are two parameter matrices: (1) theta \( (\theta) \): the residual covariance matrix and (2) nu \( (\nu) \): the observed variable intercepts.
Observed Residual Covariance Matrix (Response: Level-1)
With two observed dependent variables SYM and PA at level-1, specification of the response level is rather straightforward. Hence, the residual covariance or theta matrix is 2×2: \[ \Theta^{1,1} = \begin{bmatrix} \theta^{1,1}_{1,1} \\ \theta^{1,1}_{2,1} & \theta^{1,1}_{2,2} \end{bmatrix} \]
Superscripts make it clear that we are referring to the level-1 covariance matrix. The two subscripts indicate SYM and PA.
Observed intercept (Response: Level-1)
Because the rater and target level effects are expressed in deviation terms, mean-structure will be modeled at the response level by estimating intercepts for SYM and PA, using a nu (\( \nu \)) matrix. It is important to keep in mind that intercepts are fixed-effects or constants that are not tied to individual responses, raters, or targets. Rather, the intercepts reflect the grand-mean of the dependent variables across all levels:
\begin{bmatrix}
\nu^1_1 \\ \nu^1_2
\end{bmatrix}
\]
where \( (\nu^1_1) \) represents the grand-mean of symmetry (SYM), and \( (\nu^1_2) \) reflects the average attractiveness (PA) rating across all responses. Note that the superscripts indicate that the intercepts are at level-1.
Level-2 (Rater): Within Matrices
There are two latent variables at the rater level \( (\eta_{SYM}^R) \) & \( (\eta_{PA}^R) \) with means of zero and a variance-covariance structure described in the following psi (\Psi) matrix.
Latent Factor Covariance Matrix (Rater: Level-2)
The rater level latent covariance matrix is 2 x 2: \[ \Psi^{2,2} = \begin{bmatrix} \psi^{2,2}_{1,1} \\ \psi^{2,2}_{2,1} & \psi^{2,2}_{2,2} \end{bmatrix} \]
\( (\psi_{1,1}^{2,2}) \) is the variance of rater SYM, \( (\psi_{2,2}^{2,2}) \) is the variance of rater PA, and \( (\psi_{2,1}^{2,2}) \) is the covariance between rater SYM and PA.
Within Matrices (Rater: Level-2)
There are also two latent variables at the target level, (\( (\eta_{SYM}^T) \) & \( (\eta_{PA}^T) \)) with means of zero and a variance-covariance structure described in the following psi (\Psi) matrix.
Level-3 Latent Factor Covariance Matrix
The target level latent covariance matrix is 2 x 2: \[ \Psi^{3,3} = \begin{bmatrix} \psi^{3,3}_{1,1} \\ \psi^{3,3}_{2,1} & \psi^{3,3}_{2,2} \end{bmatrix} \]
\( (\psi_{1,1}^{3,3}) \) is the variance of target SYM, \( (\psi_{2,2}^{3,4}) \) is the variance of target PA, and \( (\psi_{2,1}^{3,3}) \) is the covariance between target SYM and PA.
Raters and photographs (targets) each have their own submodel. We now need to connect latent variables for these levels with the corresponding observed variable at the response level. In order to do so, we need two separate factor-loading matrices – one connecting the rater latent variables with the response outcomes and the second connecting the target level latent variables with the same response outcomes. This is specified by two separate across-level factor-loading matrices.
Across-Level Matrices
Rater to Response (Level-2 -> Level-1)
If you look closely, the equations and diagrams clearly indicate:
- The latent variable \( (\eta_{SYM}^R) \) in the rater level is measured by observed variable \( (SYM) \). The corresponding coefficient is 1.0.
- The latent variable \( (\eta_{SYM}^R) \) is not measured by PA. Hence, the corresponding coefficient is implicitly 0.0. For this reason, there is no path in the diagram from \( (\eta_{SYM}^R) \) to \( (PA) \).
- Similarly, the latent variable \( (\eta_{PA}^R) \) in the rater level is measured by observed variable \( (PA) \). The corresponding coefficient is 1.0.
- The latent variable \( (\eta_{PA}^R) \) for rater is not measured by \( (SYM) \). Hence, the corresponding coefficient is implicitly 0.0.
We can succinctly represent this idea by specifying the value factor-loading matrix connecting the two rater latent variables (\( (\eta^R_{SYM}) \) & \( (\eta_{PA}^R) \)) with the corresponding response variables (\( (SYM) \) & \( (PA) \)) as follows:
\begin{bmatrix}
& \eta^R_{SYM} & \eta^R_{PA} \\
SYM & 1 & 0 \\
PA & 0 & 1 \\
\end{bmatrix} \]
The rows indicate the two dependent variables and the columns indicate the two latent independent variables. While the above matrix is sufficient for the current purpose, in general we prefer to use superscripts and subscripts to indicate levels and variables.
\begin{bmatrix}
& \eta^2_1 & \eta^2_2 \\
Y^1_1 & 1 & 0 \\
Y^1_2 & 0 & 1 \\
\end{bmatrix} \]
Superscripts make it clear that the effect of first latent variable at level-2 (rater, SYM) on first observed variable at level-1 (response, \( (SYM) \)) is 1.0. Similarly, the effect of second latent variable at level-2 (rater, PA) on second observed variable at level-1 (response, \( (PA) \)) is 1.0. The remaining two effects are obviously zero. Notice that the factor loading matrix $(\Lambda{1,2}) includes superscripts to indicate that this matrix defines measurement relationship across levels 1 and 2.
In general, elements of across-level matrices have the following structure.
\begin{bmatrix}
& \eta^2_1 & \eta^2_2 \\
Y^1_1 & \lambda^{1,2}_{1,1} & \lambda^{1,2}_{1,2} \\
Y^1_2 & \lambda^{1,2}_{2,1} & \lambda^{1,2}_{2,2} \\
\end{bmatrix} \]
Note that each element has superscripts indicating which two levels are being connected and subscripts indicating which two variables are being connected. In this case, we are not estimating any factor-loadings. As such the specification of rater level to the response level factor-loading matrix is: \[ \Lambda^{1,2} = \begin{bmatrix} 1.0 & 0.0 \\ 0.0 & 1.0 \end{bmatrix} \]
Target to Response (Level-3 -> Level-1)
Factor-loading matrix connecting target latent variables with response observed variables is identical to the corresponding rater to response matrix. \[ \Lambda^{1,3} = \begin{bmatrix} 1.0 & 0.0 \\ 0.0 & 1.0 \end{bmatrix} \]
It is now apparent that with multiple levels, we need explicit superscripts to clearly indicate which two levels are being connected.
Summary Of Model Matrices
The following table provides a complete summary of pattern matrices:
| Type | Matrix | Pattern |
|---|---|---|
| level 1: \( \Theta \) |
\[
\Theta^{1,1} = \begin{bmatrix} \theta_{1,1}^{1,1} & \\ \theta_{2,1}^{1,1} & \theta_{2,2}^{1,1} \end{bmatrix} \] |
\[
\Theta^{1,1} = \begin{bmatrix} 1 \\ 1 & 1 \end{bmatrix} \] |
| level 2: \( \nu \) |
\[
\nu^1 = \begin{bmatrix} \nu_1^1 \\ \nu_2^1 \end{bmatrix} \] |
\[
\nu^1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \] |
| level 2: \( \Psi \) |
\[
\Psi^{2,2} = \begin{bmatrix} \psi_{1,1}^{2,2} \\ \psi_{2,1}^{2,2} & \psi_{2,2}^{2,2} \end{bmatrix} \] |
\[
\psi^{2,2} = \begin{bmatrix} 1 \\ 1 & 1 \end{bmatrix} \] |
| level3: \( \Psi \) |
\[
\Psi^{3,3} = \begin{bmatrix} \psi_{1,1}^{3,3} \\ \psi_{2,1}^{3,3} & \psi_{2,2}^{3,3} \end{bmatrix} \] |
\[
\Psi^{3,3} = \begin{bmatrix} 1 \\ 1 & 1 \end{bmatrix} \] |
| level-2 to level-1: \( \Lambda \) |
\[
\Lambda^{1,2} = \begin{bmatrix} \lambda_{1,1}^{1,2} & \lambda_{1,2}^{1,2} \\ \lambda_{2,1}^{1,2} & \lambda_{2,2}^{1,2} \end{bmatrix} \] |
\[
\Lambda^{1,2} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \] |
| level-3 to level-1: \( \Lambda \) |
\[
\Lambda^{1,3} = \begin{bmatrix} \lambda_{1,1}^{1,3} & \lambda_{1,2}^{1,3} \\ \lambda_{2,1}^{1,3} & \lambda_{2,2}^{1,3} \end{bmatrix} \] |
\[
\Lambda^{1,3} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \] |
The important thing to note is that all parameters for the within-level matrices are freely estimated, whereas, the two across-level factor-loading matrices have no free parameters.
Code Listing
xxM
Load xxM
xxM library needs to be loaded first. Data for the model must be available in the workspace.
library(xxm)
data(faces.xxm)
Construct R-matrices
For each parameter matrix, construct three related matrices:
- pattern matrix: A matrix indicating free or fixed parameters.
- value matrix: with start or fixed values for corresponding parameters.
- label matrix: with user friendly label for each parameter. label matrix is optional.
resp_th_pat <- matrix(c(1, 1, 1, 1), 2, 2)
resp_th_val <- matrix(c(2, 0, 0, 2), 2, 2)
resp_nu_pat <- matrix(c(1, 1), 2, 1)
resp_nu_val <- matrix(c(5, 5), 2, 1)
rater_psi_pat <- matrix(c(1, 1, 1, 1), 2, 2)
rater_psi_val <- matrix(c(0.5, 0.25, 0.25, 0.5), 2, 2)
target_psi_pat <- matrix(c(1, 1, 1, 1), 2, 2)
target_psi_val <- matrix(c(0.5, 0.25, 0.25, 0.5), 2, 2)
rater_resp_la_pat <- matrix(c(0, 0, 0, 0), 2, 2)
rater_resp_la_val <- matrix(c(1, 0, 0, 1), 2, 2)
target_resp_la_pat <- matrix(c(0, 0, 0, 0), 2, 2)
target_resp_la_val <- matrix(c(1, 0, 0, 1), 2, 2)
Construct model
xxmModel() is used to declare level names. The function returns a model object that is passed as a parameter to subsequent statements. Variable name for the return value can be abything. A
faces <- xxmModel(levels = c("response", "rater", "target"))
## A new model was created.
Add submodels
For each declared level xxmSubmodel() is invoked to add corresponding submodel to the model object. The function adds three types of information to the model object:
- parents declares a list of all parents of the current level.
- Level with the independent variable is the parent level.
- Level with the dependent variable is the child level.
- variables declares names of observed dependent (ys), observed independent (xs) and latent variables (etas) for the level.
- data R data object for the current level.
faces <- xxmSubmodel(model = faces, level = "response", parents = c("rater",
"target"), ys = c("SYM", "PA"), xs = , etas = , data = faces.response)
## Submodel for level `response` was created.
faces <- xxmSubmodel(model = faces, level = "rater", parents = , ys = , xs = ,
etas = c("rater_SYM", "rater_PA"), data = faces.rater)
## Submodel for level `rater` was created.
faces <- xxmSubmodel(model = faces, level = "target", parents = , ys = , xs = ,
etas = c("target_SYM", "target_PA"), data = faces.target)
## Submodel for level `target` was created.
Add within-level matrices
For each declared level xxmWithinMatrix() is used to add within-level parameter matrices. For each parameter matrix, the function adds the three matrices constructed earlier:
- pattern
- value
- label (optional)
faces <- xxmWithinMatrix(model = faces, level = "response", type = "theta",
pattern = resp_th_pat, value = resp_th_val, label = )
##
## 'theta' matrix does not exist and will be added.
## Added `theta` matrix.
faces <- xxmWithinMatrix(model = faces, level = "response", type = "nu", pattern = resp_nu_pat,
value = resp_nu_val, label = )
##
## 'nu' matrix does not exist and will be added.
## Added `nu` matrix.
faces <- xxmWithinMatrix(model = faces, level = "rater", type = "psi", pattern = rater_psi_pat,
value = rater_psi_val, label = )
##
## 'psi' matrix does not exist and will be added.
## Added `psi` matrix.
faces <- xxmWithinMatrix(model = faces, level = "target", type = "psi", pattern = target_psi_pat,
value = target_psi_val, label = )
##
## 'psi' matrix does not exist and will be added.
## Added `psi` matrix.
Add across-level matrices
Pairs of levels that share parent-child relationship have regression relationships. xxmBetweenMatrix() is used to add corresponding rergession matrices connecting the two levels.
- Level with the independent variable is the parent level.
- Level with the dependent variable is the child level.
For each parameter matrix, the function adds the three matrices constructed earlier:
- pattern
- value
- label (optional)
faces <- xxmBetweenMatrix(model = faces, parent = "rater", child = "response",
type = "lambda", pattern = rater_resp_la_pat, value = rater_resp_la_val,
label = )
##
## 'lambda' matrix does not exist and will be added.
## Added `lambda` matrix.
faces <- xxmBetweenMatrix(model = faces, parent = "target", child = "response",
type = "lambda", pattern = target_resp_la_pat, value = target_resp_la_val,
label = )
##
## 'lambda' matrix does not exist and will be added.
## Added `lambda` matrix.
Estimate model parameters
Estimation process is initiated by xxmRun(). If all goes well, a q&d summary of the results is printed.
faces <- xxmRun(faces)
## ------------------------------------------------------------------------------
## Estimating model parameters
## ------------------------------------------------------------------------------
## 25835.8819747542
## 25828.3989364451
## 25733.1902827389
## 25702.4713199692
## 25681.4481948706
## 25678.8606606920
## 25677.3190793148
## 25672.8671220698
## 25643.9034974637
## 25642.1922212382
## 25630.6491110205
## 25627.6566142695
## 25623.3753509948
## 25621.9737042779
## 25621.1472524671
## 25620.8412975617
## 25620.7570020643
## 25620.7376855233
## 25620.7336238756
## 25620.7332296346
## 25620.7332181517
## 25620.7332173474
## 25620.7332173226
## Model converged normally
## nParms: 11
## ------------------------------------------------------------------------------
## *
## 1: response_theta_1_1 :: 2.288 [ 0.000, 0.000]
##
## 2: response_theta_1_2 :: 0.624 [ 0.000, 0.000]
##
## 3: response_theta_2_2 :: 1.772 [ 0.000, 0.000]
##
## 4: response_nu_1_1 :: 5.207 [ 0.000, 0.000]
##
## 5: response_nu_2_1 :: 4.267 [ 0.000, 0.000]
##
## 6: rater_psi_1_1 :: 1.011 [ 0.000, 0.000]
##
## 7: rater_psi_1_2 :: 0.462 [ 0.000, 0.000]
##
## 8: rater_psi_2_2 :: 1.130 [ 0.000, 0.000]
##
## 9: target_psi_1_1 :: 0.327 [ 0.000, 0.000]
##
## 10: target_psi_1_2 :: 0.456 [ 0.000, 0.000]
##
## 11: target_psi_2_2 :: 0.916 [ 0.000, 0.000]
##
## ------------------------------------------------------------------------------
Estimate profile-likelihood confidence intervals
Once parameters are estimated, confidence intervals are estimated by invoking xxmCI(). Depending on the the number of observations and the complexity of the model, xxmCI() may take a long time to compute. xxmCI() also prints a summary of parameter estimates and CIS.
faces <- xxmCI(faces)
View results
A summary of results may be retrived as an R list by a call to xxmSummary(). The returned list has two elements:
- fit is a list with five elements:
- deviance is \( -2 Log Likelihood \) for the maximum likelihood fit function.
- nParameters is the total number of unique parameters.
- nObservations is the total number of observations across all levels.
- aic is Akaike’s Information Criterion or AIC computed as \( -2ll + 2*p \).
- bic is Bayesian Information Criterion or BIC computed as \( -2ll + p*\log(n) \).
- estimates is a single table of free parameter estimates
All xxM parameters have superscripts {child, parent} and subscripts {to, from}. xxM adds a descriptive parameter label if one is not already provided by the user.
summary <- xxmSummary(faces)
summary
## $fit
## $fit$deviance
## [1] 25621
##
## $fit$nParameters
## [1] 11
##
## $fit$nObservations
## [1] 6994
##
## $fit$aic
## [1] 25643
##
## $fit$bic
## [1] 25718
##
##
## $estimates
## child parent to from label estimate
## 1 response response SYM SYM response_theta_1_1 2.2875
## 2 response response SYM PA response_theta_1_2 0.6238
## 3 response response PA PA response_theta_2_2 1.7723
## 4 response response SYM One response_nu_1_1 5.2066
## 5 response response PA One response_nu_2_1 4.2671
## 10 rater rater rater_SYM rater_SYM rater_psi_1_1 1.0112
## 11 rater rater rater_SYM rater_PA rater_psi_1_2 0.4623
## 12 rater rater rater_PA rater_PA rater_psi_2_2 1.1299
## 17 target target target_SYM target_SYM target_psi_1_1 0.3270
## 18 target target target_SYM target_PA target_psi_1_2 0.4564
## 19 target target target_PA target_PA target_psi_2_2 0.9161
## low high
## 1 2.1793 2.4030
## 2 0.5522 0.6982
## 3 1.6885 1.8617
## 4 4.9782 5.4350
## 5 3.9292 4.6050
## 10 0.8250 1.2474
## 11 0.3087 0.6449
## 12 0.9302 1.3833
## 17 0.2066 0.5455
## 18 0.2776 0.7771
## 19 0.5987 1.4927
Free model object
xxM model object may hog a significant amount of RAM outside of R’s workspace. This memory will automatically be released, when the workspace is cleared by a call to rm(list=ls()) or at the end of the R session. Alternatively, it is recommended that xxmFree() may be called to release the memory.
faces <- xxmFree(faces)
For the current dataset, the parameter estimates are: