In this version of the model we use a conventional SEM approach to model the latent growth curve model. The data must first be in a wide format (i.e., multivariate format), with columns for each week (week 0-week 5) that contain the Hamilton depression ratings for that week. That is, for each person (row), there are 5 columns, containing values for the outcome for each time period measured.
Table of Contents
Model Equations
\[ HamD_{i1} = 1 \times \eta_{0i} + 0 \times \eta_{1i} + e_{i1} \] \[ HamD_{i2} = 1 \times \eta_{0i} + 1 \times \eta_{1i} + e_{i2} \] \[ HamD_{i3} = 1 \times \eta_{0i} + 2 \times \eta_{1i} + e_{i3} \] \[ HamD_{i4} = 1 \times \eta_{0i} + 3 \times \eta_{1i} + e_{i4} \] \[ HamD_{i5} = 1 \times \eta_{0i} + 4 \times \eta_{1i} + e_{i5} \] \[ HamD_{i6} = 1 \times \eta_{0i} + 5 \times \eta_{1i} + e_{i6} \]
In the above equations, \( i \) represents the \( i^{th} \) participant.
Alternatively, we could represent the six equations in one multivariate equation. Notice how the below equation is very similar to the equation in example 3.
\[ HamD_{iw} = 1 \times \eta_{0i} + x_w \times \eta_{1i} + e_{iw} \],
where \( w \) = 1, 2, 3, 4, 5, and 6, and \( x_w \) = 0, 1, 2, 3, 4, and 5.
\( \eta_{0i} \) is the initial status (where Hamilton depression rating is at the baseline for each participant). \( \eta_{1i} \) is the growth rate (trend).
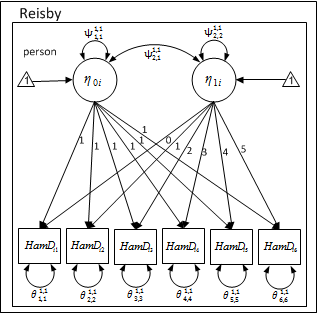
Path Diagram
xxM Model Matrices
Residual Covariance Matrix
We have six observed variables. Hence, the residual covariance or theta matrix is a (6×6) diagonal matrix:
\[
\Theta^{1,1}=
\begin{bmatrix}
\theta^{1,1}_{1,1} & \\
0 & \theta^{1,1}_{2,2} & \\
0 & 0 & \theta^{1,1}_{3,3} & \\
0 & 0 & 0 & \theta^{1,1}_{4,4} & \\
0 & 0 & 0 & 0 & \theta^{1,1}_{5,5} & \\
0 & 0 & 0 & 0 & 0 & \theta^{1,1}_{6,6} & \\
\end{bmatrix}
\]
Unlike the long format, in this case the residual variances at each occasion present themselves for our consideration. We can see them! To keep the model consistent with the one estimated in the long format, we must constrain all 6 diagonal elements to be equal
Latent Means
The latent variable mean matrix is a (2×1) matrix:
\[
\alpha^1=
\begin{bmatrix}
\alpha^1_1 & \\
\alpha^1_2
\end{bmatrix}
\]
\( \alpha_1^1 \) is the mean of \( \eta_{0i} \) (equivalent to the intercept in example 3) and \( \alpha_2^1 \) is the mean of \( \eta_{1i} \) (equivalent to the slope in example 3).
Latent Factor Covariance Matrix
The latent covariance matrix is a (2×2) matrix with two variances and single covariance:
\[
\psi^{1,1}=
\begin{bmatrix}
\psi^{1,1}_{1,1} & \\
\psi^{1,1}_{2,1} & \psi^{1,1}_{2,2}
\end{bmatrix}
\]
\( \psi_{1,1}^{1,1} \) is the variance of the initial status representing variability in \( \eta_{0i} \) across persons and \( \psi_{2,2}^{1,1} \) is the variance of the growth trend representing variability in \( \eta_{1i} \). Finally, \( \psi_{2,1}^{1,1} \) is the covariance between the two.
Lambda Matrix
The lambda matrix is 6 X 2. The rows represent the observed variables (HamD1-HamD6) and the columns represent the latent variables. As in the case of the long format, the factor loadings are not estimated. Instead these are fixed to. The first column is fixed to 1.0 and the second column is fixed to person specific values of ‘time’.
\[
\Lambda^{1,1}=
\begin{bmatrix}
\lambda^{1,1}_{1,1} & \lambda^{1,1}_{1,2} \\
\lambda^{1,1}_{2,1} & \lambda^{1,1}_{2,2} \\
\lambda^{1,1}_{3,1} & \lambda^{1,1}_{3,2} \\
\lambda^{1,1}_{4,1} & \lambda^{1,1}_{4,2} \\
\lambda^{1,1}_{5,1} & \lambda^{1,1}_{5,1} \\
\lambda^{1,1}_{6,1} & \lambda^{1,1}_{6,2} \\
\end{bmatrix}
\]
Code Listing
xxM
Matrices
Residual Covariance Matrix
For the pattern matrix of the residual covariances, we want to estimate the residual variances and we want to fix the covariances. Thus we have the following pattern matrix:
\[
\Theta^{1,1}_{pat}=
\begin{bmatrix}
1 \\
0 & 1 \\
0 & 0 & 1 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 1
\end{bmatrix}
\]
Since, we want to fix all the covariance to 0, the corresponding values are 0 in the following value matrix:
\[
\Theta^{1,1}_{val}=
\begin{bmatrix}
1000 \\
0 & 1000 \\
0 & 0 & 1000 \\
0 & 0 & 0 & 1000 \\
0 & 0 & 0 & 0 & 1000 \\
0 & 0 & 0 & 0 & 0 & 1000
\end{bmatrix}
\]
We want to set all the residual values to be equal. To do so, we use the label matrix and make all the variance the same name, such as “theta.” In xxM when parameters have the same name in a label matrix , the parameters will be constrained be equal. The covariances are equal and equal 0, so zeros as labels will work just fine here.
\[
\Theta^{1,1}_{lab}=
\begin{bmatrix}
theta \\
0 & theta \\
0 & 0 & theta \\
0 & 0 & 0 & theta \\
0 & 0 & 0 & 0 & theta \\
0 & 0 & 0 & 0 & 0 & theta
\end{bmatrix}
\]
The following code will specify the theta matrices:
th_pat <- diag(1, 6)
th_val <- diag(1000, 6)
th_lab <- diag(0, 6)
diag(th_lab) <- rep("theta", 6)
reisby.wide <- xxmWithinMatrix(reisby.wide, "subject", "theta", th_pat, th_val,
th_lab)
Latent Means
We want to freely estimate the latent means, thus the alpha pattern matrix is as follows:
\[
\alpha^1=
\begin{bmatrix}
1 \\
1
\end{bmatrix}
\]
Latent Factor Covariance Matrix
We also want to freely estimate the variances and the covariance in psi matrix, thus the psi pattern matrix is as follows:
\[
\psi^{1,1}_{pat}=
\begin{bmatrix}
1 \\
1 & 1
\end{bmatrix}
\]
Lambda Matrix
The pattern lambda matrix is 6 X 2 and is filled with all zeros, because we are fixing all the loading factors as depicted in the diagram. The complete lambda pattern matrix is as follows:
\[
\Lambda^{1,1}_{pat}=
\begin{bmatrix}
0 & 0 \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
0 & 0 \\
\end{bmatrix}
\]
The lambda matrix contains all one’s in the first column to connect the six observed variables with the initial status \( (\eta_{0i}) \) variable. The second column connects the observed variables to the growth trend variable \( (\eta_{1i}) \). The complete lambda value matrix is as follows:
\[
\Lambda^{1,1}_{val}=
\begin{bmatrix}
1 & 0 \\
1 & 1 \\
1 & 2 \\
1 & 3 \\
1 & 4 \\
1 & 5 \\
\end{bmatrix}
\]
The complete listing of xxM code is as follows:
Load xxM and data
library(xxm)
# data(reisby.wide.xxm, package='xxm')
attach("reisby.wide.xxm.RData")
Construct R-matrices
For each parameter matrix, construct three related matrices:
- pattern matrix: A matrix indicating free or fixed parameters.
- value matrix: with start or fixed values for corresponding parameters.
- label matrix: with user friendly label for each parameter. label matrix is optional.
# Subject (Level-1) matrices Theta: Residual variances (constrained to
# equality)
theta_pattern <- diag(1, 6)
theta_value <- diag(30, 6)
theta_label <- diag(0, 6)
diag(theta_label) <- rep("theta", 6)
# Psi: Latent growth factor covariance
psi_pattern <- matrix(1, 2, 2)
psi_value <- diag(c(1, 0.1), 2)
alpha_pattern <- matrix(1, 2, 1)
alpha_value <- matrix(c(23, -2), 2, 1)
# Lambda: Factor-loading matrix. Loading2 for the intercept factor (Column
# 1) fixed to 1.0 Loading2 for the slope factor (Column 2) fixed to 0.0 :
# 6.0
lambda_pattern <- matrix(0, 6, 2)
one <- rep(1, 6)
week <- seq(from = 0, to = 5, by = 1)
lambda_value <- matrix(c(one, week), 6, 2)
Construct main model object
xxmModel() is used to declare level names. The function returns a model object that is passed as a parameter to subsequent stattements.
# single level model
lgc <- xxmModel(levels = "subject")
## A new model was created.
Add submodels to the model objects
For each declared level xxmSubmodel() is invoked to add corresponding submodel to the model object. The function adds three pieces of information:
1. parents declares a list of parents of the current level.
2. variables declares names of observed dependent (ys), observed independent (xs) and latent variables (etas) for the level.
3. data R data object for the current level.
lgc <- xxmSubmodel(model = lgc, level = "subject", parents = , ys = c("depression0",
"depression1", "depression2", "depression3", "depression4", "depression5"),
xs = , etas = c("Intercept", "Slope"), data = reisby.wide)
## Submodel for level `subject` was created.
Add Within-level parameter matrices for each submodel
For each declared level xxmWithinMatrix() is used to add within-level parameter matrices. For each parameter matrix, the function adds the three matrices constructed earlier:
- pattern
- value
- label (optional)Go back to Construct-R-matrices
lgc <- xxmWithinMatrix(lgc, "subject", "theta", theta_pattern, theta_value,
theta_label)
##
## 'theta' matrix does not exist and will be added.
## Added `theta` matrix.
lgc <- xxmWithinMatrix(lgc, "subject", "psi", psi_pattern, psi_value)
##
## 'psi' matrix does not exist and will be added.
## Added `psi` matrix.
lgc <- xxmWithinMatrix(lgc, "subject", "alpha", alpha_pattern, alpha_value)
##
## 'alpha' matrix does not exist and will be added.
## Added `alpha` matrix.
lgc <- xxmWithinMatrix(lgc, "subject", "lambda", lambda_pattern, lambda_value)
##
## 'lambda' matrix does not exist and will be added.
## Added `lambda` matrix.
Add Across-level parameter matrices to the model
Pairs of levels that share parent-child relationship have regression relationships. xxmBetweenMatrix() is used to add corresponding parameter matrices connecting the two levels.
- Level with the independent variable is the parent level.
- Level with the dependent variable is the child level.
For each parameter matrix, the function adds the three matrices constructed earlier:
- pattern
- value
- label (optional)
Estimate model parameters
Estimation process is initiated by xxmRun(). If all goes well, a quick printed summary of results is produced.
lgc <- xxmRun(lgc)
## ------------------------------------------------------------------------------
## Estimating model parameters
## ------------------------------------------------------------------------------
## 2319.0477197856
## 2292.8002154702
## 2273.3646796055
## 2254.8474679323
## 2247.8056018210
## 2239.6198773428
## 2231.7775311406
## 2227.2843536626
## 2221.6455555696
## 2219.6405236648
## 2219.1151182262
## 2219.0435840622
## 2219.0407005551
## 2219.0375260183
## 2219.0375128652
## 2219.0375117621
## 2219.0375116871
## 2219.0375116526
## Model converged normally
## nParms: 6
## ------------------------------------------------------------------------------
## *
## 1: theta :: 12.217 [ 0.000, 0.000]
##
## 2: subject_psi_1_1 :: 12.629 [ 0.000, 0.000]
##
## 3: subject_psi_1_2 :: -1.421 [ 0.000, 0.000]
##
## 4: subject_psi_2_2 :: 2.079 [ 0.000, 0.000]
##
## 5: subject_alpha_1_1 :: 23.577 [ 0.000, 0.000]
##
## 6: subject_alpha_2_1 :: -2.377 [ 0.000, 0.000]
##
## ------------------------------------------------------------------------------
Estimate profile-likelihood confidence intervals
Once parameters are estimated, confidence intervals are estimated by invoking xxmCI() . Depending on the the number of observations and the complexity of the dependence structure xxmCI() may take very long. xxMCI() displays a table of parameter estimates and CIS.
View results
A summary of results may be retrived as an R list by a call to xxmSummary()
xxmSummary(lgc)
## $fit
## $fit$deviance
## [1] 2219
##
## $fit$nParameters
## [1] 6
##
## $fit$nObservations
## [1] 375
##
## $fit$aic
## [1] 2231
##
## $fit$bic
## [1] 2255
##
##
## $estimates
## child parent to from label estimate
## 1 subject subject depression0 depression0 theta 12.217
## 3 subject subject depression1 depression1 theta 12.217
## 6 subject subject depression2 depression2 theta 12.217
## 10 subject subject depression3 depression3 theta 12.217
## 15 subject subject depression4 depression4 theta 12.217
## 21 subject subject depression5 depression5 theta 12.217
## 22 subject subject Intercept Intercept subject_psi_1_1 12.629
## 23 subject subject Intercept Slope subject_psi_1_2 -1.421
## 24 subject subject Slope Slope subject_psi_2_2 2.079
## 25 subject subject Intercept One subject_alpha_1_1 23.577
## 26 subject subject Slope One subject_alpha_2_1 -2.377
## low high
## 1 10.263 14.7007
## 3 10.263 14.7007
## 6 10.263 14.7007
## 10 10.263 14.7007
## 15 10.263 14.7007
## 21 10.263 14.7007
## 22 6.954 21.3955
## 23 -3.919 0.3632
## 24 1.252 3.3661
## 25 22.492 24.6627
## 26 -2.792 -1.9619
Free model object
xxM model object may hog a large amount of RAM outside of R’s memory. This memory will automatically be released, when R’s work space is cleared by a call to rm(list=ls()) or at the end of the R session. Alternatively, xxmFree() may be called to release memory.
lgc <- xxmFree(lgc)