We now consider a general xxM model for three level data with observed and latent variables at multiple levels.
Table of Contents
Motivating Example
We may have multiple indicators of student reading achievement, teacher quality, and school resources. In this case, students are nested within teachers and teachers are nested within schools. We are interested in examining the effects of latent teacher quality and school resources on latent student achievement.
In this case, we have four observed indicators of student achievement at level-1, no observed variables at the teacher level, and three measures of school resources at level-3.
Three Level Random Intercepts Model with Latent Regression
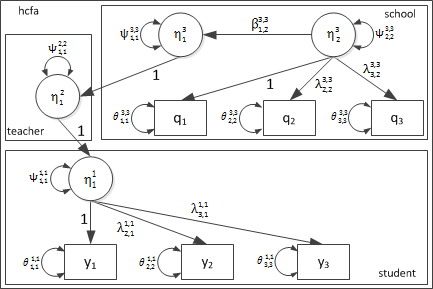
Very simply, these models are complex. It is easier to visualize these models than describe them in terms of equations or matrices. One thing to keep in mind that xxM is intended to be flexible so as to allow a model to be specified in the most natural fashion. The following model can be specified in several different equivalent ways. The simplest expression of the model is presented here.
Path Diagram
Scalar Representation
Within Level Equations
Student submodel (Level-1)
The measurement model for the student achievement can be
presented as:
\[ y_{pijk}^1=\nu_p^1 + \lambda_p^{1,1} \times \eta_{1ijk}^1 + e_{pijk}^1 \]
where, \( y_{pij} \) is \( p^{th} \) observed indicator for student \( i \), nested within teacher \( j \), nested within school \( k \) . The superscript 1 is for the student level.
\[ \eta_{1ij}^1 | \eta_{1j}^2 \sim N(0,\psi_{1,1}^{1,1}) \]
\[ e_{pij}^1 \sim N(0, \Theta^{1,1}) \]
The student model hypothesizes the following parameters:
1. \( (p-1) \) factor loadings \( (\lambda_p) \) with the first factor loading being fixed to 1.0 for scale identification.
2. Residual variance for each of the p observed indicators \( (\theta_(p,p)) \).
3. Single latent residual variance \( (\Psi_{1,1}^{1,1}). \) Note: The student level latent variable is regressed on teacher level latent factor. As a result, \( (\theta_{1,1}^{1,1}) \) is the conditional or residual variance. This is discussed later.
4. Measurement intercepts for each of the p observed indicators \( (\nu_p) \).
Teacher submodel (Level-2)
The teacher level has a single latent variable with zero mean and unknown residual variance \( (\psi_{1,1}^{2,2}). \)
The superscript 2 is for the teacher level.
\[ \eta_{1jk}^2 | \eta_{1k}^3 \sim N(0,\psi_{1,1}^{2,2}) \]
School submodel (Level-3)
The school level has two latent variables each with a mean of zero and unknown variances.
The second school level latent variable is the school-resource factor measured by three school level indicators. School level measurement model for the school-resource factor is:
\[ y_{pk}^3 = \nu_p^3 + \lambda_{2,p}^{3,3} \times \eta_{2k}^3 + e_{pk}^3 \]
\[ \eta_{2k}^3 \sim N(0,\psi_{2,2}^{3,3}) \]
\[ e_{pk}^3 \sim N(0,\Theta^{3,3}) \]
School level structural model regression latent student achievement on latent school resource factor is:
\[ \eta_{1k}^3 = \beta_{1,2}^{3,3} \times \eta_{2k}^3 + \xi_k^3 \]
\[ \xi_k^3 \sim N(0,\psi_{1,1}^{3,3}) \]
The structural model states that school level variability in student achievement is predicted by school resources. So far, our description has been limited to within-level models only. Latent variables representing random-intercepts for student achievement at the teacher and school levels were presented, but these have not yet been defined. Clearly, we need to link the latent student achievement factor
\( (\eta_{1ijk}^1) \) with the corresponding teacher level intercept \( (\eta_{1jk}^2) \). Similarly, we need to connect the school level intercept of student achievement to the student level achievement factor. There are many ways of specifying such links. Here we use a mediated effect approach. The effect of the school level intercept for student achievement on student level achievement is mediated by the teacher effect. In other words, we are envisioning regression among latent variables across levels.
Between Level Equations
Teacher To Student Effects
\[ \eta_{1ijk}^1 = \beta_{1,1}^{1,2} \times \eta_{1jk}^2 + \xi_{ijk}^1 \]
\[ \xi_{ijk}^1 \sim N(0,\psi_{1,1}^{1,1}) \]
Note:
- The dependent variable is a level-1 latent variable (student achievement). The independent variable is a level-2 latent variable (teacher intercept of latent student achievement). This is reflected in the respective superscripts.
- The superscript for the regression coefficient \( (\beta_{1,1}^{1,2}) \) indicates that the dependent variable is a level-1 variable and the independent variable is a level-2 variable.
- The subscript for the regression coefficient is (1,1) meaning the first latent variable at level-1 is being regressed on the first latent variable at level-2. With single latent variables at both levels, this seems like overkill. However, with multiple variables, superscripts and subscripts become a necessary evil.
- We return to the level-1 variance for the student achievement factor (?_1,11,1). This was incompletely specified in the student submodel.
School To Teacher Effects
\[ \eta_{1jk}^2 = \beta_{1,1}^{2,3} \times \eta_{1k}^3 \xi_{jk}^2 \]
\[ \xi_{jk}^2 \sim N(0,\psi_{1,1}^{2,2}) \]
Note:
- The dependent variable is a level-2 latent variable (teacher intercept of latent student achievement). The independent variable is a level-3 latent variable (school intercept of latent student achievement). This is reflected in the respective superscripts.
- The superscript for the regression coefficient \( (\beta_{1,1}^{2,3}) \) indicates that the dependent variable is a level-2 variable and the independent variable is a level-3 variable.
- The subscript for the regression coefficient is (1, 1) meaning the first latent variable at level-2 is being regressed on the first latent variable at level-3. In this case, we have two latent variables at level-3. Hence, we could in principle have two latent regressions coefficients (\( \beta_{1,1}^{2,3} \) & \( \beta_{1,2}^{2,3} \)). Subscripts make it clear which latent variables are involved.
- We return to the level-2 variance for the teacher achievement intercept \( (\psi_{1,1}^{2,2}) \). This was incompletely specified in the teacher sub-model.
xxM Matrix equations
The scalar representation above is complex. The actual model in matrix form is simple:
\[ y^1=\nu^1 + \lambda^{1,1} \times \eta^1 + e^1 \]
\[ \eta^1=B^{1,2} \times \eta^2 + \xi^1 \] \[ \eta^2=B^{2,3} \times \eta^3 + \xi^2 \] \[ \eta^3=B^{3,3} \times \eta^3 + \xi^3 \]
\[ e^1 \sim N(0, \Theta^{1,1}) \] \[ \xi^1 \sim N(0, \Psi^{1,1}) \] \[ \xi^2 \sim N(0, \Psi^{2,2}) \] \[ \xi^3 \sim N(0, \Psi^{3,3}) \]
Obviously, the actual structure of these matrices determines our model. The structure of each of these matrices is specified next.
xxM Model Matrices
Student submodel (Level-1)
Factor-loading matrix (Lambda)
\Lambda_{pattern}^{1,1} =
\begin{bmatrix}
0 \\
1 \\
1 \\
1
\end{bmatrix}
\]
\Lambda_{value}^{1,1} =
\begin{bmatrix}
1.0 \\
1.1 \\
0.9 \\
0.8
\end{bmatrix}
\]
The first factor-loading is fixed to 1.0. Hence, we need to fix the first parameter in the pattern matrix. The actual value at which the parameter is to be fixed is specified in the value matrix. In this case the first factor-loading is being fixed to a value of 1.0.
Observed Residual Covariance Matrix (Theta)
\Theta_{pattern}^{1,1} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\]
\Theta_{value}^{1,1} =
\begin{bmatrix}
1.1 & 0 & 0 & 0 \\
0 & 2.1 & 0 & 0 \\
0 & 0 & 1.3 & 0 \\
0 & 0 & 0 & 1.5
\end{bmatrix}
\]
Residual covariance matrix is a diagonal matrix, meaning we are only estimating residual variances. Residual covariances are all fixed to 0.0. Again we use a pattern and a value matrix to fix all off-diagonal elements to 0.0.
Latent (Residual) Covariance Matrix (PSI)
\[ \psi_{pattern}^{1,1}=[1],\psi_{value}^{1,1}=[1.1] \]
Observed Variable Intercepts (nu)
\nu_{pattern}^1 =
\begin{bmatrix}
1 \\
1 \\
1 \\
1
\end{bmatrix}
\]
\nu_{value}^1 =
\begin{bmatrix}
1.1 \\
2.1 \\
1.3 \\
0.71
\end{bmatrix}
\]
Teacher submodel (Level-2)
Latent (Residual) Covariance Matrix (PSI)
\[ \psi_{pattern}^{2,2}=[1],\psi_{value}^{2,2}=[0.05] \]
School submodel (Level-3)
Factor-loading matrix (Lambda)
\Lambda_{pattern}^{2,3} =
\begin{bmatrix}
0 & 0 \\
0 & 1 \\
0 & 1
\end{bmatrix}
\]
\Lambda_{value}^{2,3} =
\begin{bmatrix}
0.0 & 1.0 \\
0.0 & 1.1 \\
0.0 & 0.9
\end{bmatrix}
\]
There are three observed and two latent variables at level-3. Hence the factor-loading matrix is 3×2. The first latent variable is the school level random-intercept of the teacher-level random-intercept of student achievement. Clearly, the first latent variable cannot have school-level latent indicators. Hence, the first column is zero in both pattern and value matrices. The second latent variable is the school-resource factor measured by all three level-3 indicators. As always, the first factor loading is fixed to 1.0 to identify the latent measurement scale.
Observed Residual Covariance Matrix (Theta)
\Theta_{pattern}^{3,3} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{bmatrix}
\]
\Theta_{value}^{3,3} =
\begin{bmatrix}
1.1 & 0.0 & 0.0 \\
0.0 & 2.1 & 0.0 \\
0.0 & 0.0 & 1.3
\end{bmatrix}
\]
Observed Variable Intercepts (nu)
\nu_{pattern}^3 =
\begin{bmatrix}
1 \\
1 \\
1
\end{bmatrix}
\]
\nu_{value}^1 =
\begin{bmatrix}
1.1 \\
2.1 \\
0.7
\end{bmatrix}
\]
Latent variable regression matrix (Beta)
B_{pattern}^{3,3} =
\begin{bmatrix}
0 & 1 \\
0 & 0
\end{bmatrix}
\]
B_{value}^{3,3} =
\begin{bmatrix}
0.0 & 0.4 \\
0.0 & 0.0
\end{bmatrix}
\]
There are two latent variables at level-3 and the first latent variable is regressed on the second. Hence, element is freely estimated. The other three elements are fixed to zero.
Latent variable (Residual) Covariance matrix (PSI)
\psi_{pattern}^{3,3} =
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\]
,
\psi_{value}^{3,3} =
\begin{bmatrix}
0.3 & 0.0 \\
0.0 & 0.7
\end{bmatrix}
\]
Like the theta matrix, the psi matrix is a diagonal matrix. \( \psi_{1,1}^{3,3} \) is the variance of the first latent variable (student achievement random intercept) and represents the variance in the intercept factor unexplained by the school-resource factor. \( \psi_{1,1}^{3,3} \) is the unconditional variance of the school-resource factor.
Teacher To Student Effects (Level 2 to Level 1)
Latent Variable Regression Matrix (Beta)
\[ B_{pattern}^{1,2} = [0], B_{value}^{1,2} = [1.0] \]
This matrix links the teacher latent random-intercept variable with the student latent achievement variable. As indicated earlier, the value is fixed to 1.0. Note that the superscript has two elements, the first element refers to the lower level (student) and the second element refers to the higher level (teacher). This is always true for all linking matrices.
School To teacher Effects (Level 3 to Level 2)
Latent Variable Regression Matrix (Beta)
B_{pattern}^{2,3} =
\begin{bmatrix}
0 & 0
\end{bmatrix}
\]
B_{value}^{2,3} =
\begin{bmatrix}
1.0 & 0.0
\end{bmatrix}
\]
This matrix links the school latent random-intercept of student achievement with the teacher latent intercept of achievement variable. There is a single latent variable at level-2 (teacher random-intercept of student achievement), but two latent variables at level-3 (school random-intercept of student achievement and school-resources). Only the school random-intercept of student achievement influences the teacher random intercept of student achievement. Hence, the first element is fixed to 1.0 and second element is fixed to 0.0.
Model Matrices Summary
The following table provides a complete summary of parameter matrices:
| Type | Matrix | Pattern |
|---|---|---|
| level 1: \( \Theta \) |
\[
\Theta^{1,1} = \begin{bmatrix} \theta_{1,1}^{1,1} \\ \theta_{2,1}^{1,1} & \theta_{2,2}^{1,1} \\ \theta_{3,1}^{1,1} & \theta_{3,2}^{1,1} & \theta_{3,3}^{1,1} \\ \end{bmatrix} \] |
\[
\Theta^{1,1} = \begin{bmatrix} 1 \\ 0 & 1 \\ 0 & 0 & 1 \\ \end{bmatrix} \] |
| level 2: \( \nu \) |
\[
\nu^{1} = \begin{bmatrix} \nu_1^1 \\ \nu_2^1 \\ \nu_3^1 \end{bmatrix} \] |
\[
\nu^{1} = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} \] |
| level 2: \( \Lambda \) |
\[
\Lambda^{1,1} = \begin{bmatrix} \lambda_{1,1}^{1,1} \\ \lambda_{2,1}^{1,1} \\ \lambda_{3,1}^{1,1} \end{bmatrix} \] |
\[
\Lambda^{1,1} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} \] |
| level1: \( \Psi \) |
\[
\Psi^{2,2} = [\psi_{1,1}^{2,2}] \] |
\[
\Psi^{2,2} = [1] \] |
| level-2 to level-1: \( B \) |
\[
B^{1,2}_{1,1} = \begin{bmatrix} beta_{1,1}^{1,2} \end{bmatrix} \] |
\[
B^{1,2} = [0] \] |
| level 2: \( \Psi \) |
\[
\Psi^{2,2} = \begin{bmatrix} psi_{1,1}^{2,2} \end{bmatrix} \] |
\[
\Psi^{2,2} = [1] \] |
| level 3: \( \Theta \) |
\[
\Theta^{3,3} = \begin{bmatrix} \theta_{1,1}^{3,3} & \\ \theta_{2,1}^{3,3} & \theta_{2,2}^{3,3} \\ \theta_{3,1}^{3,3} & \theta_{3,2}^{3,3} & \theta_{3,3}^{3,3} \end{bmatrix} \] |
\[
\Theta^{3,3} = \begin{bmatrix} 1 \\ 0 & 1 \\ 0 & 0 & 1 \end{bmatrix} \] |
| level 3: \( \nu \) |
\[
\nu^{3} = \begin{bmatrix} \nu_1^3 \\ \nu_2^3 \\ \nu_3^3 \\ \end{bmatrix} \] |
\[
\nu^{3} = \begin{bmatrix} 1 \\ 1 \\ 1 \\ \end{bmatrix} \] |
| level 3 -> level 2: \( B \) |
\[
B^{2,3} = \begin{bmatrix} \beta_{1,1}^{2,3} \\ \end{bmatrix} \] |
\[
B^{2,3} =[0] \] |
| level 3 -> level 2: \( \Lambda \) |
\[
\Lambda^{3,3} = \begin{bmatrix} \lambda_{1,1}^{3,3} \\ \lambda_{2,1}^{3,3} \\ \lambda_{3,1}^{3,3} \\ \end{bmatrix} \] |
\[
\Lambda^{3,3} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ \end{bmatrix} \] |
| level 3: \( B \) |
\[
B^{3,3} = \begin{bmatrix} \beta_{1,1}^{3,3} \\ \beta_{2,1}^{3,3} & \beta_{2,2}^{3,3} \end{bmatrix} \] |
\[
B^{1,2} = \begin{bmatrix} 0 \\ 1 & 0 \\ \end{bmatrix} \] |
| level 3: \( \Psi \) |
\[
\Psi^{2,2} = \begin{bmatrix} \psi_{1,1}^{3,3} &\\ \psi_{2,1}^{3,3} & \psi_{2,2}^{3,3} \end{bmatrix} \] |
\[
\Psi^{2,2} = \begin{bmatrix} 1 & \\ 0 & 1 \end{bmatrix} \] |
Code Listing
xxM
The complete listing of xxM code is as follows:
Load xxM and data
library(xxm)
data(hcfa.xxm)
Construct R-matrices
For each parameter matrix, construct three related matrices:
- pattern matrix: A matrix indicating free or fixed parameters.
- value matrix: with start or fixed values for corresponding parameters.
- label matrix: with user friendly label for each parameter. label matrix is optional.
# Student: factor-loading matrix
ly1_pat <- matrix(c(0, 1, 1), 3, 1)
ly1_val <- matrix(c(1, 1.1, 0.9), 3, 1)
ly1_lab <- matrix(c("ly1", "ly2", "ly3"), 3, 1)
# Student: factor-covariance matrix
ps1_pat <- matrix(1, 1, 1)
ps1_val <- matrix(0.498, 1, 1)
# Student: observed residual-covariance matrix
th1_pat <- diag(1, 3)
th1_val <- diag(c(2.727, 2.99, 2.854), 3)
# Student: 'grand-means' NU
nu1_pat <- matrix(1, 3, 1)
nu1_val <- matrix(c(0.526, 0.571, 0.592), 3, 1)
# Teacher model matrices Teacher: factor-covariance matrix
ps2_pat <- matrix(1, 1, 1)
ps2_val <- matrix(0.1333, 1, 1)
# School model matrices School: factor-loading matrix
ly3_pat <- matrix(c(0, 0, 0, 0, 1, 1), 3, 2)
ly3_val <- matrix(c(0, 0, 0, 1, 0.9, 1.1), 3, 2)
# School: factor-covariance matrix
ps3_pat <- matrix(c(1, 0, 0, 1), 2, 2)
ps3_val <- matrix(c(0.1335, 0, 0, 0.1402), 2, 2)
# School: observed residual-covariance matrix
th3_pat <- diag(1, 3)
th3_val <- diag(c(1.787, 1.937, 2.418), 3)
# School: 'grand-means/intercepts' NU
nu3_pat <- matrix(1, 3, 1)
nu3_val <- matrix(c(0.129, 0.144, 0.081), 3, 1)
# School: 'Latent Factor Regression' Beta
be3_pat <- matrix(c(0, 0, 1, 0), 2, 2)
be3_val <- matrix(c(0, 0, 0.3, 0), 2, 2)
# Teacher -> Student matrices
be12_pat <- matrix(0, 1, 1)
be12_val <- matrix(1, 1, 1)
# School - > teacher matrices
be13_pat <- matrix(0, 1, 2)
be13_val <- matrix(c(1, 0), 1, 2)
Construct main model object
xxmModel() is used to declare level names. The function returns a model object that is passed as a parameter to subsequent stattements.
hcfa <- xxmModel(levels = c("student", "teacher", "school"))
## A new model was created.
Add submodels to the model objects
For each declared level xxmSubmodel() is invoked to add corresponding submodel to the model object. The function adds three pieces of information:
1. parents declares a list of parents of the current level.
2. variables declares names of observed dependent (ys), observed independent (xs) and latent variables (etas) for the level.
3. data R data object for the current level.
hcfa <- xxmSubmodel(model = hcfa, level = "student", parents = c("teacher"),
ys = c("y1", "y2", "y3"), xs = , etas = c("Eta_y_Stu"), data = hcfa.student)
## Submodel for level `student` was created.
hcfa <- xxmSubmodel(model = hcfa, level = "teacher", parents = c("school"),
ys = , xs = , etas = c("Eta_y_Tea"), data = hcfa.teacher)
## Submodel for level `teacher` was created.
hcfa <- xxmSubmodel(model = hcfa, level = "school", parents = , ys = c("q1",
"q2", "q3"), xs = , etas = c("Eta_y_Sch", "Eta_q_Sch"), data = hcfa.school)
## Submodel for level `school` was created.
Add Within-level parameter matrices for each submodel
For each declared level xxmWithinMatrix() is used to add within-level parameter matrices. For each parameter matrix, the function adds the three matrices constructed earlier:
- pattern
- value
- label (optional)Go back to Construct-R-matrices
## Student within matrices (lambda, psi, theta and nu)
hcfa <- xxmWithinMatrix(model = hcfa, level = "student", "lambda", pattern = ly1_pat,
value = ly1_val, )
##
## 'lambda' matrix does not exist and will be added.
## Added `lambda` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "student", "psi", pattern = ps1_pat,
value = ps1_val, )
##
## 'psi' matrix does not exist and will be added.
## Added `psi` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "student", "theta", pattern = th1_pat,
value = th1_val, )
##
## 'theta' matrix does not exist and will be added.
## Added `theta` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "student", "nu", pattern = nu1_pat,
value = nu1_val, )
##
## 'nu' matrix does not exist and will be added.
## Added `nu` matrix.
## Teacher within matrices (psi)
hcfa <- xxmWithinMatrix(model = hcfa, level = "teacher", type = "psi", pattern = ps2_pat,
value = ps2_val, )
##
## 'psi' matrix does not exist and will be added.
## Added `psi` matrix.
## School within matrices (psi)
hcfa <- xxmWithinMatrix(model = hcfa, level = "school", type = "lambda", pattern = ly3_pat,
value = ly3_val, )
##
## 'lambda' matrix does not exist and will be added.
## Added `lambda` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "school", type = "psi", pattern = ps3_pat,
value = ps3_val, )
##
## 'psi' matrix does not exist and will be added.
## Added `psi` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "school", type = "theta", pattern = th3_pat,
value = th3_val, )
##
## 'theta' matrix does not exist and will be added.
## Added `theta` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "school", type = "nu", pattern = nu3_pat,
value = nu3_val, )
##
## 'nu' matrix does not exist and will be added.
## Added `nu` matrix.
hcfa <- xxmWithinMatrix(model = hcfa, level = "school", type = "beta", pattern = be3_pat,
value = be3_val, )
##
## 'beta' matrix does not exist and will be added.
## Added `beta` matrix.
Add Across-level parameter matrices to the model
Pairs of levels that share parent-child relationship have regression relationships. xxmBetweenMatrix() is used to add corresponding parameter matrices connecting the two levels.
- Level with the independent variable is the parent level.
- Level with the dependent variable is the child level.
For each parameter matrix, the function adds the three matrices constructed earlier:
- pattern
- value
- label (optional)
## Teacher->Student beta matrix
hcfa <- xxmBetweenMatrix(model = hcfa, parent = "teacher", child = "student",
type = "beta", pattern = be12_pat, value = be12_val, )
##
## 'beta' matrix does not exist and will be added.
## Added `beta` matrix.
## School-> Teacher beta matrix
hcfa <- xxmBetweenMatrix(model = hcfa, parent = "school", child = "teacher",
type = "beta", pattern = be13_pat, value = be13_val, )
##
## 'beta' matrix does not exist and will be added.
## Added `beta` matrix.
Estimate model parameters
Estimation process is initiated by xxmRun(). If all goes well, a quick printed summary of results is produced.
hcfa <- xxmRun(hcfa)
## ------------------------------------------------------------------------------
## Estimating model parameters
## ------------------------------------------------------------------------------
## 7273.8992243320
## 7252.2353906918
## 7222.6287229552
## 7155.1359798539
## 7139.6561567329
## 7136.8767770611
## 7136.1068385479
## 7135.4722284233
## 7135.0147225173
## 7133.1257527536
## 7132.1586514570
## 7131.2099648536
## 7127.9873687812
## 7125.4389500312
## 7122.3889403682
## 7119.7323670317
## 7118.4376730549
## 7117.1537751747
## 7116.4620115001
## 7115.0030056260
## 7114.0481233927
## 7113.3427515510
## 7112.7216360541
## 7112.3058493205
## 7111.1493314690
## 7110.5603623814
## 7109.4898387721
## 7109.2963024781
## 7108.6388375998
## 7108.4795710352
## 7108.3081919555
## 7108.2475296169
## 7108.0417326562
## 7107.9236649660
## 7107.8607037744
## 7107.8412157275
## 7107.8298330672
## 7107.8278998368
## 7107.8278611623
## 7107.8278550066
## 7107.8278541925
## 7107.8278541190
## 7107.8278541116
## Model converged normally
## nParms: 21
## ------------------------------------------------------------------------------
## *
## 1: student_theta_1_1 :: 1.664 [ 0.000, 0.000]
##
## 2: student_theta_2_2 :: 2.001 [ 0.000, 0.000]
##
## 3: student_theta_3_3 :: 1.896 [ 0.000, 0.000]
##
## 4: student_psi_1_1 :: 0.555 [ 0.000, 0.000]
##
## 5: student_nu_1_1 :: 0.526 [ 0.000, 0.000]
##
## 6: student_nu_2_1 :: 0.571 [ 0.000, 0.000]
##
## 7: student_nu_3_1 :: 0.592 [ 0.000, 0.000]
##
## 8: student_lambda_2_1 :: 0.936 [ 0.000, 0.000]
##
## 9: student_lambda_3_1 :: 0.907 [ 0.000, 0.000]
##
## 10: teacher_psi_1_1 :: 0.372 [ 0.000, 0.000]
##
## 11: school_theta_1_1 :: 0.625 [ 0.000, 0.000]
##
## 12: school_theta_2_2 :: 1.039 [ 0.000, 0.000]
##
## 13: school_theta_3_3 :: 1.521 [ 0.000, 0.000]
##
## 14: school_psi_1_1 :: 0.350 [ 0.000, 0.000]
##
## 15: school_psi_2_2 :: 0.635 [ 0.000, 0.000]
##
## 16: school_nu_1_1 :: 0.129 [ 0.000, 0.000]
##
## 17: school_nu_2_1 :: 0.144 [ 0.000, 0.000]
##
## 18: school_nu_3_1 :: 0.081 [ 0.000, 0.000]
##
## 19: school_lambda_2_2 :: 0.597 [ 0.000, 0.000]
##
## 20: school_lambda_3_2 :: 0.667 [ 0.000, 0.000]
##
## 21: school_beta_1_2 :: 0.784 [ 0.000, 0.000]
##
## ------------------------------------------------------------------------------
Estimate profile-likelihood confidence intervals
Once parameters are estimated, confidence inetrvals are estimated by invoking xxmCI() . Depending on the the number of observations and the complexity of the dependence structure xxmCI() may take very long. xxMCI() displays a table of parameter estimates and CIS.
View results
A summary of results may be retrived as an R list by a call to xxmSummary()
summary <- xxmSummary(hcfa)
summary
## $fit
## $fit$deviance
## [1] 7108
##
## $fit$nParameters
## [1] 21
##
## $fit$nObservations
## [1] 1920
##
## $fit$aic
## [1] 7150
##
## $fit$bic
## [1] 7267
##
##
## $estimates
## child parent to from label estimate
## 1 student student y1 y1 student_theta_1_1 1.66378
## 3 student student y2 y2 student_theta_2_2 2.00119
## 6 student student y3 y3 student_theta_3_3 1.89591
## 7 student student Eta_y_Stu Eta_y_Stu student_psi_1_1 0.55522
## 8 student student y1 One student_nu_1_1 0.52624
## 9 student student y2 One student_nu_2_1 0.57135
## 10 student student y3 One student_nu_3_1 0.59219
## 12 student student y2 Eta_y_Stu student_lambda_2_1 0.93636
## 13 student student y3 Eta_y_Stu student_lambda_3_1 0.90679
## 15 teacher teacher Eta_y_Tea Eta_y_Tea teacher_psi_1_1 0.37223
## 18 school school q1 q1 school_theta_1_1 0.62531
## 20 school school q2 q2 school_theta_2_2 1.03868
## 23 school school q3 q3 school_theta_3_3 1.52076
## 24 school school Eta_y_Sch Eta_y_Sch school_psi_1_1 0.34956
## 26 school school Eta_q_Sch Eta_q_Sch school_psi_2_2 0.63518
## 27 school school q1 One school_nu_1_1 0.12905
## 28 school school q2 One school_nu_2_1 0.14366
## 29 school school q3 One school_nu_3_1 0.08124
## 34 school school q2 Eta_q_Sch school_lambda_2_2 0.59705
## 35 school school q3 Eta_q_Sch school_lambda_3_2 0.66653
## 38 school school Eta_y_Sch Eta_q_Sch school_beta_1_2 0.78377
## low high
## 1 1.41097 1.9462
## 3 1.73207 2.3065
## 6 1.64215 2.1845
## 7 0.38487 0.7649
## 8 0.20716 0.8453
## 9 0.26673 0.8760
## 10 0.29696 0.8874
## 12 0.80386 1.0876
## 13 0.77508 1.0572
## 15 0.20484 0.6295
## 18 0.00100 1.2865
## 20 0.54740 1.7356
## 23 0.84988 2.5259
## 24 0.00100 0.8394
## 26 0.12313 1.6997
## 27 -0.22740 0.4855
## 28 -0.21344 0.5008
## 29 -0.34507 0.5075
## 34 0.05989 1.9900
## 35 0.02505 2.2614
## 38 0.26477 2.0330
Free moodel object
xxM model object may hog a large amount of RAM outside of R’s memory. This memory will automatically be released, when R’s workspace is cleared by a call to rm(list=ls()) or at the end of the R session. Alternatively, xxmFree() may be called to release memory.
hcfa <- xxmFree(hcfa)
For the current dataset, the parameter estimates are:
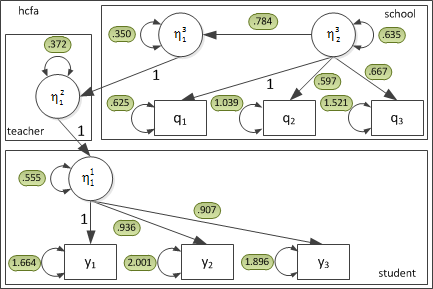
Mean structure is not illustrated in this diagram. The student and school \( \nu \) matrices were estimated as:
\nu^{1} =
\begin{bmatrix}
.526 & \\
.571 \\
.592 \\
\end{bmatrix}
\]
and
\nu^{1} =
\begin{bmatrix}
.129 & \\
.144 \\
.081 \\
\end{bmatrix}
\]